
Both appear similar but the axes differ). You you can calculate it yourself with his excellent Shiny app (be aware of the differences between the graphs from the figure above and that provided in the App. Inserting these values into the equation gives: Both are output parameters from G*Power (see figure below). The critical t value is t crit = 1.974, and the noncentrality parameter δ is δ = 3.279. Given a two-sided t test, α = 0.05, 86 observations per group gives an actual power of 90%. However, until then I should say that I am not sure how generalizable this is to other tests. I would be happy about any useful comments and explanations though. I do not know exactly how and why it works because I lack the statistical knowledge. I derived this formula working with the examples provided by Mr. T crit is the critical t value that is output by the an a priori or ex-post power analysisĭ is the actual or observed power given α and n effect size To transform this critical t value (t crit) to a critical d value (d crit, or d SESOI), I came up with the following formula:ĭ SESOI is the smallest effect size of interest, i.e.
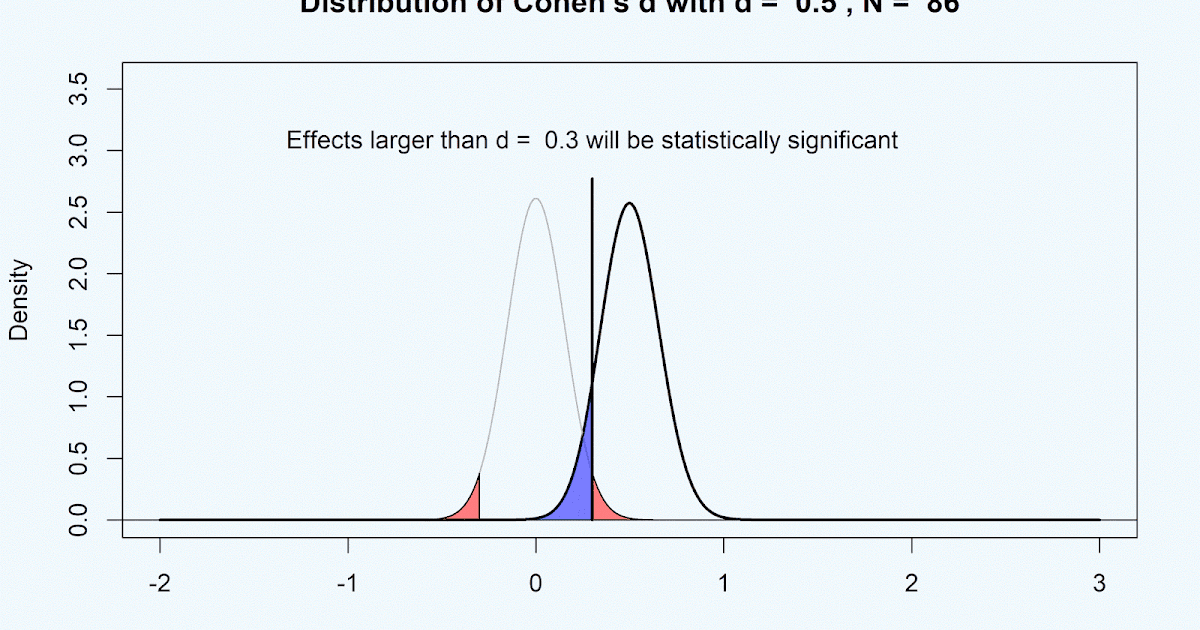
When your t value is right of this, you reject the null hypothesis either correctly or incorrectly because, depending on whether there is a true effect or not, you fall into one of the four cells depicting the relationship between null hypothesis and the decision about the null hypothesis. Thinking of the graph output by G*Power: the green line shows the critical t value left of which is a blue area that depicts the Type II error rate. What you want to find, basically, is the critical d instead of the critical t. G*Power does not provide the SESOI directly, but you can calculate it easily by hand with the information G*Power provides. Possibly this is equivalent to the SESOI.
#Gpower effect size trial#
If you want to register a randomized controlled trial at the AEA RCT Registry you are asked to calculate the minimum detectable effect size (MDES) of your most important analyses. However, sometimes it is important to know what the SESOI is. The former calculations provides you with the information that you need 86 participants per group, while the latter calculates a power of 0.9 given a sample size of 172 (86 per group) with the above values. Even though it is not advised for good reasons, G*Power also allows you to calculate the observed (post hoc) power given the observed effect size, the number of observations, and α. Usually, I use G*Power in order to infer how many observations I need to detect an expected effect size d, say 0.5, with α = 0.05 and 90% power using a two-sided t test. Go to hi Shiny app to have a look at the graph. This is the value that is equivalent to the critical t value you know from the respective figures from G*Power. From this it is possible to infer the critical d-value. To do this he visualizes a power analysis for a two-tailed t test by plotting the distribution of Cohen’s d given n participants per group, effect size d, and alpha level α = 0.05.
#Gpower effect size how to#
In his post he explains how to infer the smallest effect size of interest (SESOI) from a power analysis. Lakens is an experimental psychologist at the Human-Technology Interaction group at Eindhoven University of Technology, The Netherlands. My instruction is largely based on an excellent blog post from a blog named “The 20% Statistician” by Daniel Lakens. In this post I give a brief instruction on how to calculate the smallest effect size of interest with output from G*Power.


 0 kommentar(er)
0 kommentar(er)
